Attractor Reconstruction using Delay Coordinates

Introduction

Complex systems, e.g. in biology, often have a high number of dimensions, but we are only able to observe some of them. For instance, we might be able to track the concentration of some selected proteins in a cell over time; however, it is not possible to track the behaviour of the complete system that gives rise to these dynamics (which would require tracking dozens or hundreds of proteins over time, out of which we might not even know all the relevant ones yet).

This gives rise to an interesting question: Given only time-series observations of some of a system's elements, can we somehow reconstruct the dynamics of the complete system? As it turns out, this is very much possible using the method of delays, where we use our observations to construct a space with additional dimensions (the so-called embedding space) by using time delayed values of the measurements that are available to us.

This approach was recently explained to me by one of my PhD advisors, and I instantly found it extremely fascinating. Thus, I did some reading on the topic and played around with the approach. In this post, I want to summarise what I have learned for future reference and in order to expose more people to this fascinating method.

Selecting the number of embedding dimensions

Takens' theorem provides a sufficient condition under which an attractor of box-counting dimension \(d\) can be reconstructed from such delay coordinates. This is possible if we have a set of \(k\) coordinates with \(k > 2d\), however it should be noted that in some cases like the Lorenz system in the example below, less coordinates can also suffice. The strange attractor of the Lorenz system has a box-counting dimension of \( d \approx 2.1\), so the reconstruction is only guaranteed to work for at least \(k=5\) delay coordinates; however in practice even \(k=2\) already yields a very good reconstruction, as we will see below.

In practice, we naturally do not know the exact properties of the system our observations are coming from. Thus, in particular we do not know the system's intrinsic dimensionality, and accordingly we have to come up with an estimate of how many delay coordinates to use based on the observed time series. This is still an area of ongoing research with a large body of literature existing, so we will not go into any more detail here.

Selecting the optimal delay

Selecting an appropriate delay \(\Delta t\) is crucial for obtaining a useful embedding. Fraser and Swinney proposed using the mutual information in order to determine an appropriate delay. Specifically, they recommended selecting the delay at which the mutual information reaches its first local minimum. Other approaches exist as well, for instance it is possible to select the optimal delay based on the autocorrelation of the generated time series.

Trying it

Let's try this approach using the Lorenz system, which is a three-dimensional dynamical system given by the following set of coupled differential equations:

\(\dot x(t) = \sigma (y(t)-x(t))\)

\(\dot y(t) = x(t) (\rho - z(t)) - y(t)\)

\(\dot z(t) = x(t) y(t) - \beta z(t)\)

The system generally has a so-called "strange" attractor, which is an attractor that has a fractal structure. This strange attractor additionally is chaotic, meaning that its behaviour depends on the initial conditions of the system in a very senstivite manner. In a typical case \((\rho = 28, \sigma = 10, \beta = 8/3)\), a solution of the systems looks as follows:

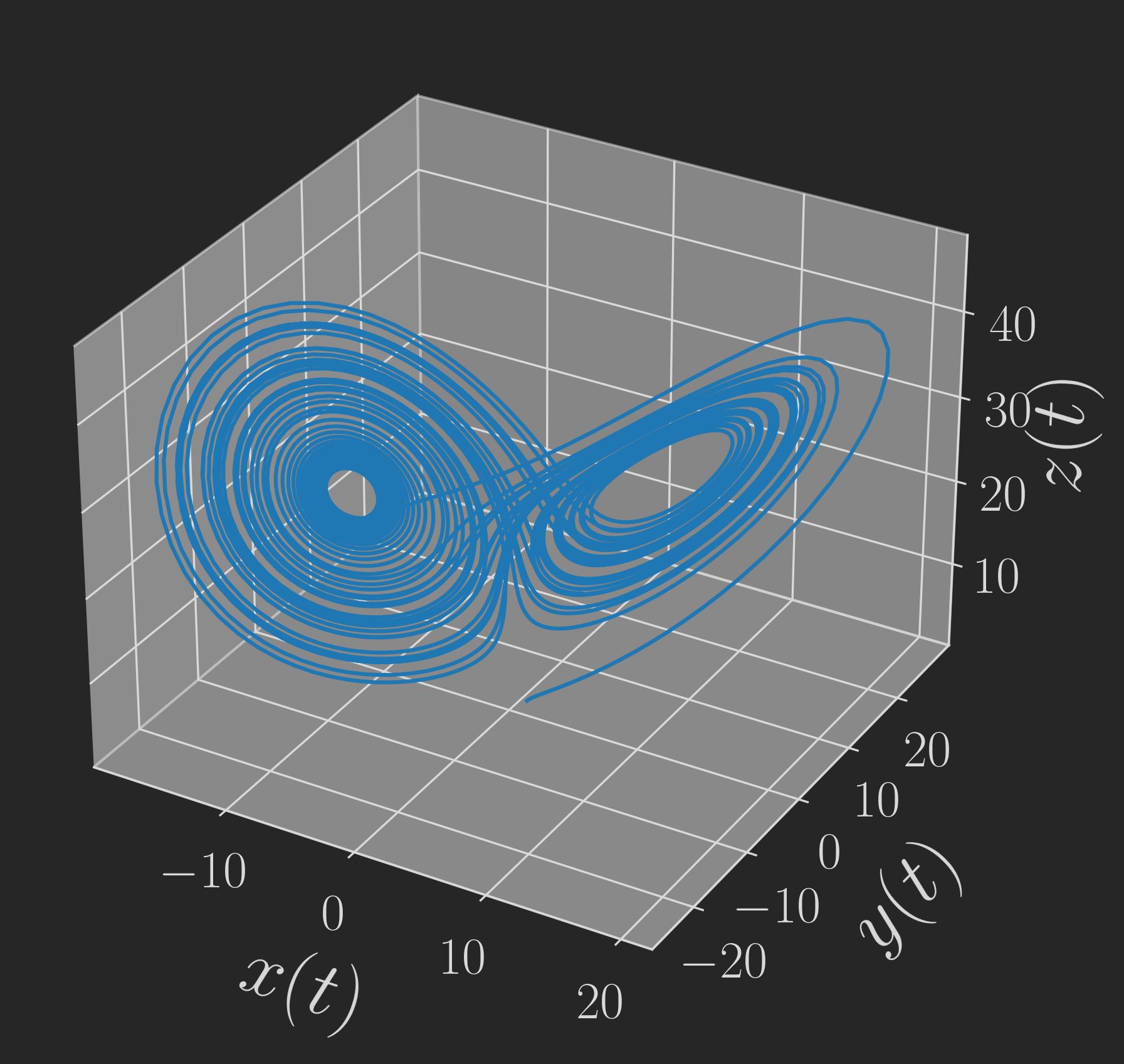
Let's now assume that we have only a time series of values for \(x(t)\), which might look as follows:

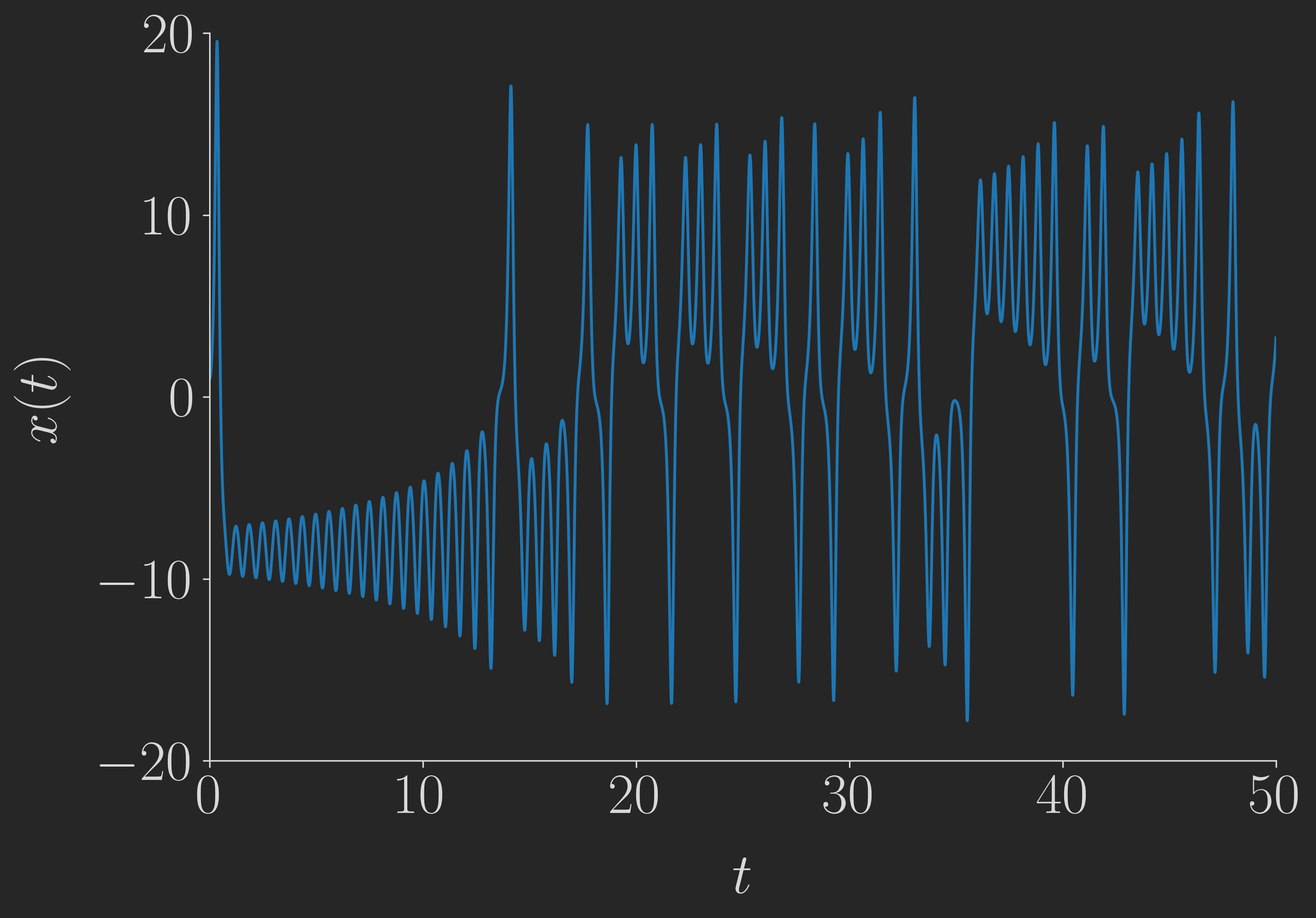
Now, we want to reconstruct the complete attractor from this time-series alone in two dimensions by using delay coordinates. The following little animation shows how such a 2d delay embedding \((x(t), x(t+\Delta t))\) looks for different delays:

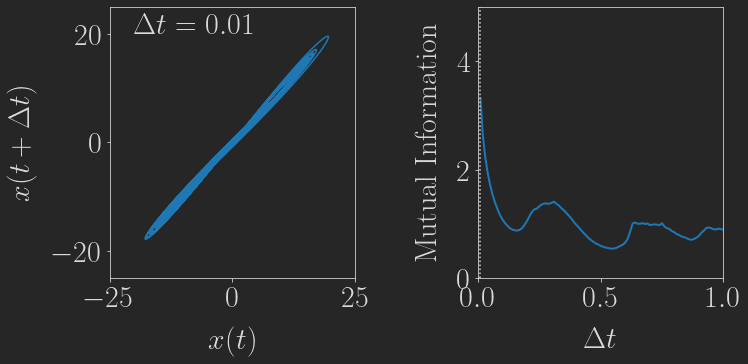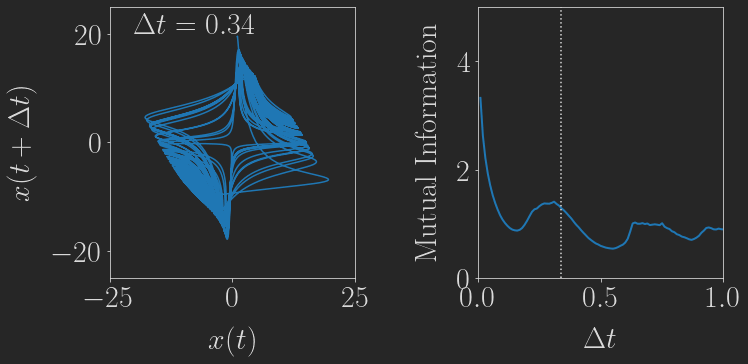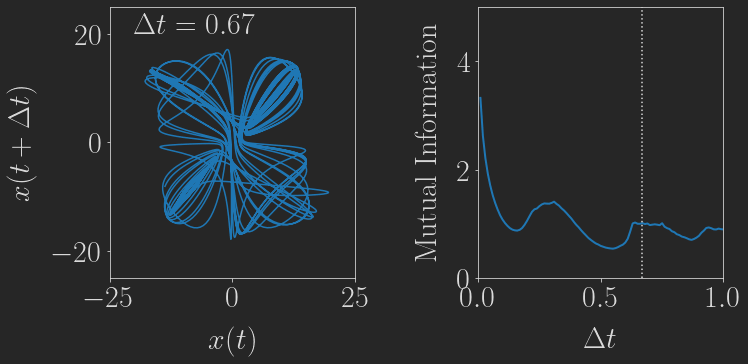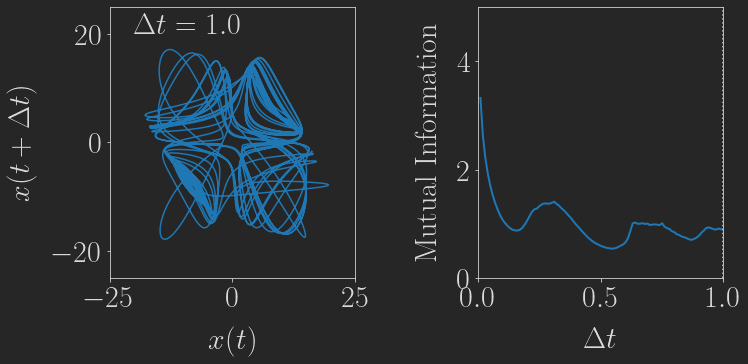
Based on the mutual information, a delay of \(\Delta t \approx 0.16\) seems to be the most suitable, and indeed this embedding looks reasonably similar to the real thing shown above, although a slightly smaller delay would be even better in my opinion.

Conclusions

We have seen that it is indeed possible to reconstruct an attractor from partial observations by using delay coordinates. Selecting optimal delay parameters (number of delay coordinates, amount of delay) is non-trivial, topic of ongoing research and depends on the specific application.